Very well, this is really more of a mathematics than a physics post, but so what. Besides, equations of this nature do pop up in physics problems from time to time.
Question (variants of which often appear on Quora): How do you solve the equation, \(x^a=b^x\)?
Equations of the type
$$x^a=b^x$$
do not usually have solutions in terms of elementary functions, but they can be solved with the help of Lambert's W-function.
The W-function is defined as the solution to the equation
$$W(z)e^{W(z)} = z.$$
Which means that any equation that can be brought to the form \(x e^x = {\rm const.}\) can be solved using \(W(z).\)
So let's do a bit of algebra:
$$\begin{align*}
x^a &= b^x,\\
a\ln x &= x\ln b,\\
(1/x)\ln x &= (1/a)\ln b,\\
(1/x)\ln(1/x) &= -(1/a)\ln b.
\end{align*}$$
Now let \(y=\ln(1/x),\) so that \(x=1/e^y.\) Then,
$$ye^y = -(1/a)\ln b,$$
so we can now solve for \(y\) in terms of the W-function:
$$y=W(-(\ln b)/a).$$
We also note that \(e^{W(z)}=z/W(z),\) which follows from the definition of the W-function. With this we get, for \(x,\)
$$x=\dfrac{1}{e^y}=-\dfrac{a}{\ln b}W\left(-\dfrac{\ln b}{a}\right).$$
This is the general solution.
Here is one specific example: \(x^5=8^x.\) So let \(a=5\) and \(b=8.\) Then we have
$$x=-\dfrac{5}{\ln 8}W\left(-\dfrac{\ln 8}{5}\right)\simeq 2.207-1.183i.$$
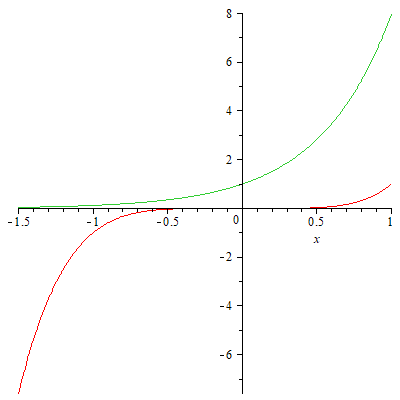
Yes, that is a complex number. This particular equation has no real solution. This can be seen easily if we plot the curves \(x^5\) (red) and \(8^x\) (green), as we can see that they do not intersect anywhere:
Additionally, the solution can also be extended to equations of the form
$$cx^a=b^x.$$
These equations can be brought to the previous form as follows:
$$\begin{align*}
cx^a &= b^x\\
(c^{1/a}x)^a &= b^x\\
(c^{1/a}x)^a &= b^{c^{-1/a} c^{1/a} x}\\
(c^{1/a}x)^a &= (b^{c^{-1/a}})^{c^{1/a} x}
\end{align*}$$
Now let
$$\begin{align*}
X &= c^{1/a}x,\\
B &= b^{c^{-1/a}},
\end{align*}$$
and the equation becomes
$$X^a = B^X,$$
which we already know how to solve:
$$X=-\dfrac{a}{\ln B}W\left(-\dfrac{\ln B}{a}\right).$$
Substituting \(A\) and \(X\) and noting that \(\ln B=c^{-1/a}\ln b\), we get
$$\begin{align*}
c^{1/a}x &= -\dfrac{a}{c^{-1/a} \ln b} W\left(-\dfrac{c^{-1/a} \ln b}{a}\right),\\
x &= -\dfrac{a}{\ln b}W\left(-\dfrac{\ln b}{ac^{1/a}}\right).
\end{align*}$$
One additional caveat concerns the ambiguity arising from the the properties of exponentiation. For instance, the equation \(2^x=x^2\) has three real solutions, but the above formalism would yield only two of them (and we get those two because the W-function itself has multiple real values for part of its real domain.) To obtain the third solution, we must recognize that \(x^2=(-x)^2\), so we must also solve \(2^{-y}=y^2\), i.e., \((1/2)^y=y^2\), with \(x=-y\). This yields the third real solution, at \(x\simeq -0.766665\).
And, of course, there are infinitely many complex solutions, corresponding to the various branches of the W-function.