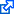Given a four-potential $A_\mu$, the Maxwell tensor is
$$F_{\mu\nu}=\nabla_\mu A_\nu-\nabla_\nu A_\mu=\partial_\mu A_\nu-\partial_\nu A_\mu.$$
Using the language of exterior forms, it is trivially easy to write down Maxwell's equations, and recognize them as geometric identities:
\begin{align}
F&={\rm d}A,\\
{\rm d}F={\rm d^2}A&=0,\\
{\star{\rm d}}{\star F}&=J,\\
{\star{\rm d}}{\star J}={\star{\rm d}}{\star}{\star{\rm d}}{\star F}={\star{\rm d}^2}{\star F}&=0.
\end{align}
It turns out that it is also possible to spell out a generally covariant form of Maxwell's equations using the conventional indexed tensor notation. To do so, we first note that
$$\partial_\mu\sqrt{-g}=\Gamma^\kappa_{\kappa\mu}\sqrt{-g},$$
so for a vector field, it is true that
$$\partial_\mu(\sqrt{-g}A^\mu)=(\partial_\mu\sqrt{-g})A^\mu+\sqrt{-g}A^\mu{}_{,\mu}=\sqrt{-g}(A^\mu{}_{,\mu}+\Gamma^\kappa_{\kappa\mu}A^\mu)=\sqrt{-g}\nabla_\mu A^\mu.$$
Similar formulae can be developed for differential forms (and for totally antisymmetric tensors). For instance:
$$\partial_\kappa[\sqrt{-g}(A^{\mu\kappa}-A^{\kappa\mu})]=\Gamma^\lambda_{\lambda\mu}\sqrt{-g}(A^{\mu\kappa}-A^{\kappa\mu})+\sqrt{-g}(A^{\mu\kappa}{}_{,\kappa}-A^{\kappa\mu}{}_{,\kappa})=\sqrt{-g}\nabla_\kappa(A^{\mu\kappa}-A^{\kappa\mu}).$$
Using the above result, we can write the divergence of the Maxwell tensor as
$$g^{\mu\kappa}\nabla_\kappa F_{\mu\nu}=g_{\lambda\nu}\nabla_\kappa F^{\kappa\lambda}=\frac{1}{\sqrt{-g}}g_{\lambda\nu}\partial_\kappa(\sqrt{-g}F^{\kappa\lambda}),$$
which we can do because $F^{\kappa\lambda}$ is totally antisymmetric. This divergence defines the current, i.e.,
$$\frac{1}{\sqrt{-g}}\partial_\kappa(\sqrt{-g}F^{\kappa\lambda})=\frac{1}{\sqrt{-g}}\partial_\kappa[\sqrt{-g}g^{\kappa\mu}g^{\lambda\nu}(\partial_\mu A_\nu-\partial_\nu A_\mu)]=J^\lambda.$$
These are Maxwell's equations known commonly in the form $\nabla\cdot\vec{E}=\rho$, $\nabla\times\vec{B}-\partial\vec{E}/\partial t=\vec{j}$.
To see how this form can be recovered, let us work in Minkowski spacetime ($g_{\mu\nu}={\rm diag}(+1,-1,-1,-1)$, $\sqrt{-g}=1$) and in Cartesian coordinates, in which case
$$F_{\mu\nu}=\begin{pmatrix}0&E_x&E_y&E_z\\-E_x&0&-B_z&B_y\\-E_y&B_z&0&-B_x\\-E_z&-B_y&B_x&0\end{pmatrix},$$
and
$$\partial_\mu F^{\mu\nu}=\begin{pmatrix}\partial/\partial t&~&\nabla&~\end{pmatrix}\cdot\begin{pmatrix}0&-E_x&-E_y&-E_z\\E_x&0&-B_z&B_y\\E_y&B_z&0&-B_x\\E_z&-B_y&B_x&0\end{pmatrix}=\begin{pmatrix}\nabla\cdot\vec{E}\\~\\-\partial\vec{E}/\partial t+\nabla\times\vec{B}\\~\end{pmatrix}=\begin{pmatrix}\rho\\~\\\vec{j}\\~\end{pmatrix}.$$
Current conservation is given by the equation $\nabla_\lambda J^\lambda=0$, which we can also write, after multiplying by $\sqrt{-g}$, as
$$\partial_\lambda(\sqrt{-g}J^\lambda)=0,$$
or
$$\partial_\lambda\partial_\kappa[\sqrt{-g}g^{\kappa\mu}g^{\lambda\nu}(\partial_\mu A_\nu-\partial_\nu A_\mu)]=0.$$
In the case of the Minkowski metric and Cartesian coordinates, this becomes the well-known conservation equation $\partial\rho/\partial t-\nabla\cdot\vec{j}=0$.
For the other two Maxwell equations, we form the dual of $F_{\mu\nu}$:
$$G^{\mu\nu}=\frac{1}{\sqrt{-g}}\epsilon^{\mu\nu\kappa\lambda}F_{\kappa\lambda},$$
where $\epsilon^{\mu\nu\kappa\lambda}$ is the totally antisymmetric Levi-Civita symbol and the extra division by $\sqrt{-g}$ is required to turn it into a unit antisymmetric tensor in curved spacetime. The divergence of this (pseudo-)tensor is zero:
$$\nabla_\mu G^{\mu\nu}=0.$$
Once again, since $G^{\mu\nu}$ is also a totally antisymmetric tensor, this expression can be written as
$$\partial_\mu(\sqrt{-g}G^{\mu\nu})=\partial_\mu[\epsilon^{\mu\nu\kappa\lambda}(\partial_\mu A_\nu-\partial_\nu A_\mu)]=0.$$
These are Maxwell's equations that we normally write in the form, $\partial\vec{B}/\partial t-\nabla\times\vec{E}=0$, $\nabla\cdot\vec{B}=0$. To see how, once again we can use Minkowski spacetime and Cartesian coordinates. Spelling out the components of the dual of the Maxwell-tensor, we get
$$G^{\mu\nu}=\begin{pmatrix}0&-B_x&-B_y&-B_z\\B_x&0&-E_z&E_y\\B_y&E_z&0&-E_x\\B_z&-E_y&E_x&0\end{pmatrix}.$$
The divergence of this tensor is given by
$$\partial_\mu G^{\mu\nu}=\begin{pmatrix}\partial/\partial t&~&\nabla&~\end{pmatrix}\cdot\begin{pmatrix}0&-B_x&-B_y&-B_z\\B_x&0&-E_z&E_y\\B_y&E_z&0&-E_x\\B_z&-E_y&E_x&0\end{pmatrix}=\begin{pmatrix}\nabla\cdot\vec{B}\\~\\-\partial\vec{B}/\partial t+\nabla\times\vec{E}\\~\end{pmatrix}=0.$$
To sum up, whereas these three-dimensional forms of Maxwell's equations are valid only in flat spacetime with a Cartesian coordinate system, the following forms of Maxwell's equations are generally covariant and, better yet, they are expressed in a form that is free of covariant derivatives or Christoffel-symbols:
| $$\frac{1}{\sqrt{-g}}\partial_\kappa(\sqrt{-g}F^{\kappa\lambda})=J^\lambda,$$ | Gauss's law and Ampère's law; | |
| $$\partial_\lambda(\sqrt{-g}J^\lambda)=0,$$ | conservation law; | |
| $$\partial_\mu(\epsilon^{\mu\nu\kappa\lambda}F_{\kappa\lambda})=0,$$ | Gauss's law for magnetism, Faraday's law. |