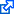The acceleration, coordinate time, proper time and distance fields are editable; the rest are calculated whenever an edited value changes and the cursor leaves the field (e.g., by tabbing to the next field.)
| Quantity | Value | Units | Expression |
|---|---|---|---|
| Acceleration | $a,$ | ||
| Coordinate time | $\displaystyle t=\frac{c}{a}\text{sh}\frac{aT}{c}=\sqrt{\left(\frac{d}{c}\right)^2 + 2\frac{d}{a}},$ | ||
| Proper time | $\displaystyle T=\frac{c}{a}\text{sh}^{-1}\frac{at}{c}=\frac{c}{a}\text{ch}^{-1}\left(\frac{ad}{c^2}+1\right),$ | ||
| Distance | $\displaystyle d=\frac{c^2}{a}\left(\text{ch}\frac{aT}{c}-1\right)=\frac{c^2}{a}\left(\gamma-1\right),$ | ||
| Velocity | $\displaystyle v=c~\text{th}\frac{aT}{c}=\frac{at}{\gamma},$ | ||
| Gamma-factor | $\displaystyle\gamma=\text{ch}\frac{aT}{c}=\sqrt{1+\left(\frac{at}{c}\right)^2}=\frac{ad}{c^2} + 1.$ |
Discussion
This calculator is a straightforward implementation of one of the oldest Internet physics FAQs in existence, the Relativistic Rocket FAQ.
That classic FAQ offers additional details, such as computing the gross vs. net weight ratio (i.e., the amount of fuel a rocket would have to carry even if it was a "perfect" rocket with a lossless photon drive).